PyCaretを用いた機械学習とサンプルコード
本投稿は,PyCaret[1]を用いた機械学習の行い方と,そのサンプルコードに関する投稿です.本投稿で説明に用いた,Pythonモジュール(samplML.py)や学習用のデータ(training_data.csv)は,筆者のGitHubアカウント[2]にて,公開しています.
本投稿の開発環境は,PyCaret v3.3.2を用いています.また,サンプルコードを書いた2025年8月16日時点で,PyCaretがサポートしているPythonのバージョンはv3.9系~3.11系であるため,Pythonはv3.10.11を用いました.
本投稿の,機械学習における各アルゴリズムや指標の説明に関しては,末尾の参考文献に記載する技術ブログ[3]を参照しており,内容が重複しています.これは,管理者によって削除されいつアクセスできなくなってもおかしくないWebサイト/ページの性質に対し,本投稿の筆者自身の手元に情報を記録として残す備忘録を目的としているためです.
目次
1. 機械学習の流れ
1.1 機械学習の流れ
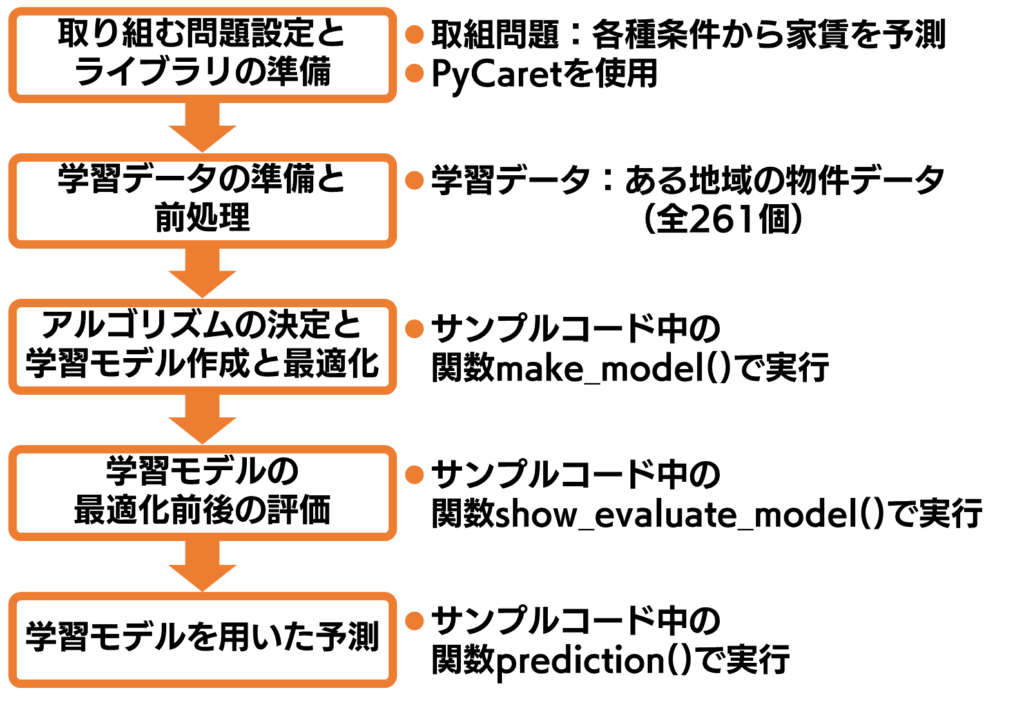
図1に示す機械学習の流れに沿い,サンプルコードを抜粋しながら第2章~第6章で説明する.
サンプルコードをはじめとする諸ファイルとそのディレクトリ構造は下記の通りである.サンプルコードにおいては,実行に必要なファイルは実行ファイルと同じディレクトリに格納しておく必要がある.また,サンプルコードによって生成されるファイルは,実行ファイルと同じディレクトリに格納されるようにしてある.
./
├ finalized_model.pkl :作成したモデル.サンプルコード実行後に生成される
├ logs.log :ログファイル.サンプルコード実行後に生成される
├ prediction_data.csv :家賃を予測したい各特徴量の条件を記入したもの
├ result.txt :予測結果を記載したファイル.サンプルコード実行後に生成される
├ sample_ML.py :サンプルコード.実行ファイル
└ training_data.csv :学習データ
1.2 用語の定義
本投稿で扱う用語の定義を行う.機械学習では,”モデル”という用語がしばしば扱われるが,下記のように文脈によって指すものが異なる.
- 入力した学習データに基づき学習し作成したモデル
- その学習・モデル作成に用いたモデル(例:ランダムフォレスト,勾配ブースティング)
これらを区別するべく,本投稿では,作成したモデルを”学習モデル”または”モデル”と呼称する.そして学習やモデル作成に用いたモデルを”学習アルゴリズム”または”アルゴリズム”と呼称する.
2. 取り組む問題設定とライブラリの準備
機械学習で問題解決する際,そもそもどのような問題を扱うのかによって,用いるアルゴリズムが異なる.扱う問題を大別すると表1に示す例があげられる.
| 回帰 | ||
|
||
| 分類 | ||
|
||
| クラスタリング | ||
|
||
| 異常検知 | ||
|
ライブラリは,PyCaretを扱う.そしてPyCaretで回帰問題を扱う際は,下記コードでインポートできる.importの記述方法において,ワイルドカードを用いず具体的に1つ1つ記述している理由は,PEP8にて非推奨とされていることと,Sphinxを用いたドキュメント生成を行う場合を考慮したためである[4].
from pycaret.regression import setup, compare_models, pull, create_model, tune_model, finalize_model, save_model, plot_model, predict_model, load_model3. 学習データの準備と前処理
3.1 学習データの準備
本投稿で扱う学習データ(training_data.csv)は,筆者が調べたある地域の実際の物件のデータ(全261個)をまとめたものである.特徴量は,表2に示す4つである.そして目的変数(予測したい対象)は,表3の通りである.
機械学習には,内挿と外挿の概念がある.内挿は,学習したデータの範囲内で予測を行う.これに対し外挿は,学習したデータの範囲外で予測を行う.機械学習は,基本として内挿の範囲でのみ予測を行うものである.そのため,本投稿で紹介するサンプルコードと学習データを扱う際は,各特徴量に対し,表1にて示した値の範囲内で予測を行われたし.
| 特徴量 | 値の範囲 | |
| 駅までの徒歩時間[分] |
|
|
| 面積[m^2] |
|
|
| 部屋の階数[階] |
|
|
| 築年数[年] |
|
|
| 特徴量 | 値の範囲 | |
| 家賃[万円] |
|
|
サンプルコードは,学習データの形式がCSVファイル(文字コード:UTF-8,BOM無し)を前提に作ってある.筆者が用意したtraining_data.csvを編集する際は,注意されたし.
3.2 学習データの準備
前処理に関しては,本投稿では基本として省略する.
そのうえで前処理とはどのようなものか簡略的な説明だけする.例えば学習データに,性別に関する特徴量があり,”男性”/”女性”という値を持っていたとする.これらは数値データなく文字データであり,機械学習での処理が困難なため,”男性”=0,”女性”=1のように数値に置き換える.
4. アルゴリズムの決定と学習モデル作成と最適化
サンプルコードでは,クラスsampleMLのクラス関数make_model()にて,アルゴリズムの決定と学習モデル作成と最適化を行う.
4.1 アルゴリズムの決定
PyCaretの関数compare_models()を用いて,各アルゴリズムの各指標における結果を比較する.本投稿では,比較結果の中でR^2の指標に着目し,R^2の値が最も大きかったアルゴリズムが自動的に採用されるよう,下記のようにコーディングしている.
# アルゴリズムの比較
compare_models() # アルゴリズムごとの比較結果を表示
df_compare_models_result = pull() # PyCaretの関数pull()は,直前に実行したPyCarertの処理結果を取得する
self.ml_algorithm = df_compare_models_result.loc[df_compare_models_result["R2"].idxmax()] # R^2の値が最も大きいアルゴリズムを採用するこの関数compare_models()は,各アルゴリズムの比較する際,内部的に各アルゴリズムを用いてモデルを作成し比較している.そのため,「作成した学習モデルが学習データをどれだけ説明できているか」の評価指標であるR^2が,この関数compare_models()で各アルゴリズムを比較する際の指標の1つとしてあげられている.
関数compare_models()における学習アルゴリズム名および指標に関し,それぞれ説明する表4および表5を,第4.3節に示す.用いるアルゴリズム名を指定する場合は,表4の”ID”の項目に記載した名称を下記のように引数として与える.
self.created_model = create_model("et") # 任意のアルゴリズムでモデルを作成したい場合の例("et"は,Extremely Randomized Trees)4.2 学習モデルの作成
PyCaretの関数create_model()を用いて,指定したアルゴリズムでモデルを作成するよう,下記のようにコーディングしている.
そして作成したモデルに対し,PyCaretの関数tune_model()を用いて最適化・ハイパーパラメータのチューニングを行う.場合によっては,最適化は不要な操作である.引数のn_iterは,ハイパーパラメータの組み合わせを試行する反復回数である.計算時間とトレードオフの関係にあり,デフォルトは10である.引数のoptimizeは,最適化を行う観点である.
# 指定したアルゴリズムでモデルを作成
self.created_model = create_model(self.ml_algorithm.name) # アルゴリズムの比較で求めたR^2が最大のアルゴリズムを用いる
self.tuned_model = tune_model(self.created_model, n_iter = 10, optimize = "r2") # モデルの最適化
self.finalized_model = finalize_model(self.tuned_model) # モデルの確定
save_model(self.finalized_model, model_name = "finalized_model") # 作成したモデルをファイルとして保存.load_modelで読み込めば,以後もこのモデルを使用可能4.3 学習アルゴリズム名および指標の説明
| ID | 概要 | |
| catboost |
|
|
| gbr |
|
|
| et |
|
|
| rf |
|
|
| xgboost |
|
|
| lightgbm |
|
|
| ada |
|
|
| lr |
|
|
| ridge |
|
|
| lar |
|
|
| br |
|
|
| dt | ||
| et |
|
|
| lasso |
|
|
| huber |
|
|
| omp |
|
|
| knn |
|
|
| llar |
|
|
| par |
|
|
| ard |
|
|
| ransac |
|
|
| tr |
|
|
| kr |
|
|
| svm |
|
|
| mlp |
|
|
| 指標名(略称) | 概要 | |
| MAE |
|
|
| MSE |
|
|
| RMSE |
|
|
| R2 |
|
|
5. 学習モデルの最適化前後の評価
5.1 学習モデルの最適化前後の評価
サンプルコードでは,クラスsampleMLのクラス関数show_evaluate_model()にて,作成したモデルに対し最適化の前と後の評価を図示する.作成したモデルの良し悪しや,より良いモデルを作成するための判断に用いるものであり,クラス関数show_evaluate_model()の処理は省いても機械学習と予測自体は可能である.
サンプルコードでは,数ある指標の中から”学習曲線”,”実測値と予測値”,”特徴量の訓練への寄与”の3つの指標で,最適化の前と後のそれぞれの評価と図示を行っている(計6個の図示).
# モデルの最適化前
print("最適化前の「学習曲線」「実測値と予測値」「特徴量の訓練への寄与」を図示")
plot_model(self.created_model, scale = 4, plot = "learning") # 学習曲線の図示
plot_model(self.created_model, scale = 4, plot = "error") # 予測誤差の図示
plot_model(self.created_model, scale = 4, plot = "feature") # 特徴量の重要度の図示
# モデルの最適化後
print("最適化後の「学習曲線」「実測値と予測値」「特徴量の訓練への寄与」を図示")
plot_model(self.tuned_model, scale = 4, plot = "learning") # 学習曲線の表示
plot_model(self.tuned_model, scale = 4, plot = "error") # 予測誤差の図示
plot_model(self.tuned_model, scale = 4, plot = "feature") # 特徴量の重要度の図示5.2 関数plot_model()の説明
関数plot_model()に伴う,実行環境ごとの挙動の違いを表6に示す.また,関数plot_model()で図示できる各指標の説明を,表7~表8に示す.
| 実行環境 | 挙動 | |
| Terminal (例:GNOME-terminalからPythonファイルを実行した場合) |
|
|
| Spyder(IDE) |
|
|
| Visual Studio Code(エディタ) |
|
|
| Cooks Distance Plot(クックの距離,ID:cooks)[3] | ||
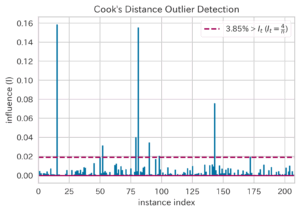 |
|
|
| Prediction Error Plot(予測誤差プロット,ID:error)[3] | ||
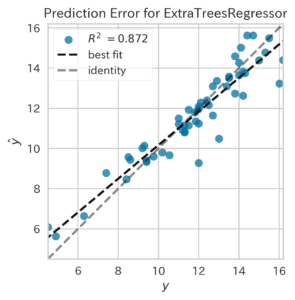 |
|
|
| Feature Importance(top 10)(特徴量の重要度(上位10個の特徴量),ID:feature)[3] | ||
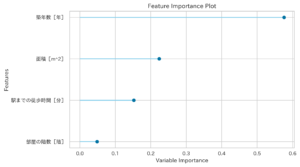 |
|
|
| Feature Importance(all)(特徴量の重要度(全ての特徴量),ID:feature_all)[3] | ||
|
||
| Learning Curve(学習曲線,ID:learning)[3] | ||
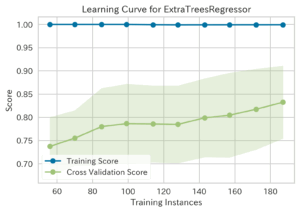 |
|
|
| Manifold Learning(多様体学習,ID:manifold) | ||
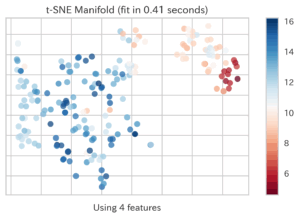 |
|
|
| Residuals Plot(残差プロット,ID:residuals)[3] | ||
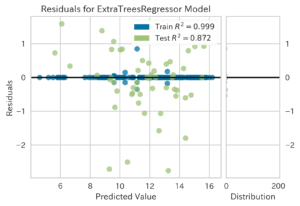 |
|
|
| Recursive Feature Selection(RFS,再帰的特徴選択,ID:rfe)[3] | ||
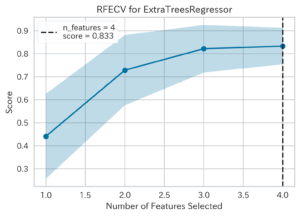 |
|
|
| Validation Curve(検証曲線,ID:vc) | ||
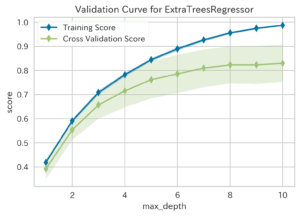 |
|
|
| ハイパーパラメータ | 横軸が取るハイパーパラメータ | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. 学習モデルを用いた予測
サンプルコードでは,クラスsampleMLのクラス関数prediction()にて,目的変数に対する予測を行う.
df_target = pd.read_csv("prediction_data.csv", encoding = "utf-8") # 予測させたい条件の読み込み
self.df_predicted = predict_model(self.finalized_model, data = df_target) ”駅までの徒歩時間”,”面積”,”部屋の階”,”築年数”の各特徴量がどのような条件の場合の家賃を予測したいかを,サンプルコードでは実行前にprediction_data.csvに記入しておく必要がある(図2).
図2に示したprediction_data.csvには,目的変数である”家賃”の列が設けてある.これは,コード中の学習データを格納した二次元の行列や,予測したい条件を格納した二次元の行列など,各行列の列数を統一し扱いを楽にする目的のためである.そして,”家賃”は目的変数であるため,どのような数値を入力しても予測に影響しない.他方で,列数の変化が生じないよう某かの値を入力しておく必要があるため,図2に示す通り”0”を入力してある.
prediction_data.csvは,training_data.csvと同様に,文字コードがUTF-8(BOM無し)のCSVファイルである.
7. 各種Tips
7.1 実行時間の短縮(モデル作成時の各設定)
機械学習における実行時間の大半を,モデルの作成に対する処理が占める.そしてモデル作成に要する時間に影響を与える要素として,特徴量の数や,ハイパーパラメータのチューニングにおける反復数があげられる.サンプル数が多く,偏りも無い場合は,チューニングの反復数を少なくすることも,実行時間の短縮手段の1つとしてあげられる.
7.2 実行時間の短縮(DataFrame型変数に対する操作)
DataFrame型の変数などで扱うデータセットに対し,代入や演算などの操作を行う場合は,for文を用いて一行一行確認し操作をするのではなく,ベクトル化によってデータセット全体に一括処理を行うことで,実行時間の短縮を期待できる.
for文を用いる場合,Pythonのインタプリタが1つ1つの反復処理を実行する.この過程で,オーバーヘッド(元の目的の処理に対し,追加で発生する処理)が生じるため,処理が遅くなる.これに対し,ベクトル化された操作では,低レベル言語で書かれたライブラリによってデータ全体を処理するため,Pythonのオーバーヘッドが発生しない.
また,メモリアクセスの観点でも,高速化の効果が期待できる.for文は,データに対し逐次アクセスを行う.これに対しベクトル化された操作は,連続したメモリ領域に一括で操作を行うことができる.これによりキャッシュのヒット率が上がり,処理速度が向上する.
7.3 関数plot_model()で出力する図のサイズを大きく/小さくしたい場合
関数plot_model()引数に”scale”を与える.これは,出力する図の大きさに対し,倍率を指定し調整する引数であり,デフォルト値は1である.筆者・サンプルコードにおいては,出力した図を本投稿で用いる目的で,scale = 4に拡大している.
plot_model(self.tuned_model, scale = 4, plot = "learning") # 学習曲線の表示7.4 関数plot_model()で出力する図中の日本語文字が文字化けした場合の解決方法
Python向けのグラフ描画ライブラリであるMatplotlibのインストールとその日本語化をすることで,解決できる.まず,下記コマンドをコンソール等に入力し,Matplotlibの日本語パッケージを開発環境にインストールする.
pip install japanize_matplotlibその後,機械学習のコーディングを行っているPythonファイル上で,Matplotlibやその日本語モジュールを,下記のようにインポートする.
import matplotlib.pyplot as plt
import japanize_matplotlib
7.5 機械学習やPyCaretに関し筆者が参照したことのあるもの
- Pycaret全般
- アルゴリズムLight Gradient Boosting
- 分類問題
- モデルの評価
参考文献
- Home – PyCaret, PyCaret, https://pycaret.org/, (参照2025-8-15).
- YANAKA Shunsuke, ynksnk/makeDocumentsBySphinx, GitHub, https://github.com/ynksnk/machineLearningSampleCode, (参照2025-8-15).
- Shugigashi, PyCaretの初心者向けまとめ(回帰編) #Python – Qiita, Qiita Inc., https://qiita.com/shuhigashi/items/0fb37468e64c76f4b245, (参照2025-8-15).
- PythonコードのドキュメントをdocstringとSphinxを用いて自動生成する方法 – word in the world, word in the world, https://word-in-the-world.com/2025/01/31/docstring-and-sphinx/,(参照2025-8-15).
- Takumi_Fukuda(福田 琢巳), 簡単にできる機械学習 ~PyCaretを使ってみた~ #Python – Qiita, Qiita Inc., https://qiita.com/Takumi_Fukuda/items/99e60793ac700974cfc4, (参照2025-8-18).
- 2g, Pycaretの使い方, クラスメソッド株式会社, https://zenn.dev/ottantachinque/articles/2022-05-05_pycaret, (参照2025-8-18).
- mitama (id:nigimitama), LightGBMの「No further splits with positive gain」というwarningの意味 – 盆暗の学習記録, 株式会社はてな, https://nigimitama.hatenablog.jp/entry/2021/01/05/205741, (参照2025-8-18).
- Shugigashi, PyCaretの初心者向けまとめ(分類編) #Python – Qiita, Qiita Inc., https://qiita.com/shuhigashi/items/cb6816a1da1d347bbdc2, (参照2025-8-18).
- ground0state(abetan), Pycaretの回帰・分類で出力されるグラフの種類について解説, Qiita Inc., https://qiita.com/ground0state/items/57e565b23770e5a323e9, (参照2025-8-18).