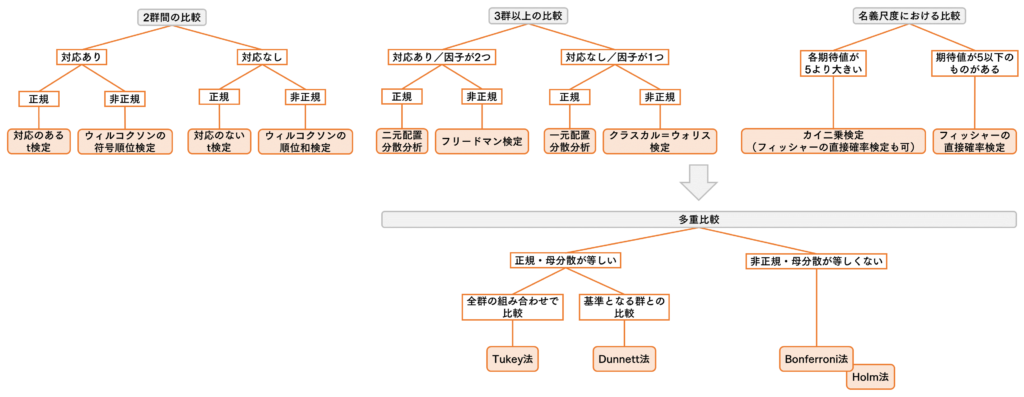
統計検定における目的に応じた検定法の早見表

　本投稿は，統計検定において，実験プロトコルやその目的に応じて使用可能な検定法を判断するための，早見表です（図1）．

2群間の比較

t検定（対応のあるt検定／対応のないt検定）

使用例
対応のある場合：同一被験者における，ある薬を投与する前とした後の比較
対応のない場合：ある薬を投与した男性と女性の比較
使用条件
対応：対応あり／対応なし
母集団の分布：正規分布

ウィルコクソンの符号順位検定

使用例
同一被験者における，ある薬を投与する前とした後の比較
使用条件
対応：対応あり
母集団の分布：非正規分布でも可能

ウィルコクソンの順位和検定（「マン＝ホイットニーのU検定）

使用例
ある刺激を提示した際の，異なる被験者間での経時的な計測値（e.g. 脈拍，体温）の比較
使用条件
対応：対応なし
母集団の分布：非正規分布でも可能

　本章で例示した検定手法は，2群間の比較においてのみ使用し，3群以上の比較に使用してはならない．その理由について，説明する．

A群・B群・C群の比較に対し，2群間の比較に用いるt検定を行ったとする（有意水準 p＜0.05）
この場合「A群とB群」「A群とC群」「B群とC群」の組み合わせで3回比較することになる
ここで有意水準5%の検定を3回重ねて行うということは「1-0.95^3≒0.14」となり，5%でなく約14%の確率で第1種の過誤が起きる検定をしていることになる
過誤
「差は無いのに差がある」と判定してしまうことを，第1種の過誤と呼ぶ．これに対し「差があるのに差は無い」と判定してしまうことを，第2種の過誤と呼ぶ

3群以上の比較

分散分析（ANOVA：Analysis of variance）

使用例
対応のある場合：同一の被験者に対する，ある刺激の提示前・提示後の比較
対応のない場合：ある刺激を提示した，若年者群・中年者群・高年者群の3つの群間比較
使用条件
対応：対応あり（二元配置分散分析）／対応なし（一元配置分散分析）
母集団の分布：正規分布
（非正規分布の場合は，対応ありならばフリードマン検定，対応なしならばクラスカル＝ウォリス検定などの検定法があげられる）

　　分散分析における各用語等の説明を，以下に記載する．

要因
母平均に差を与えるもののこと．噛み砕いて言うと，結果に影響を与える要素のこと，計測値を変化させる原因，人為的な条件設定による実験要因など
「因子」と呼ばれる場合もあるが，おそらくこの「要因」と同義だと思われる
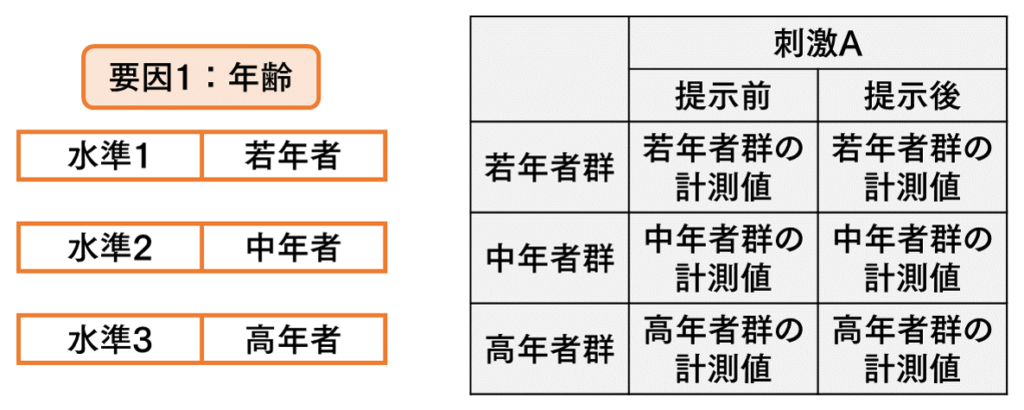
例えば図2のように，実験全体で用いる刺激が1種だけ且つ提示の有／無でなく前後の比較ならば，結果に差異を与える要素は年齢（若年者／中年者／高齢者）のため，年齢の観点からの「要因は1」となる．そしてこれを「一元配置」と呼ぶ（図2）
水準
要因に含まれる群の数のこと．要因を構成する条件．1要因は最低でも2水準で構成される
例えば図2のように，ある1つの刺激の提示を，若年者群・中年者群・高年者群の3つの群それぞれに行うならば，「水準は3」となる

一元配置と二元配置
一元配置分散分析は，対応のない比較に用いられる．二元配置分散分析は，交互作用（因子が互いに影響を及ぼしているか）を判断する際に用いる（図3）
ただし，「同一の被験者に対する，ある刺激の提示前・提示後」のような対応ある比較の場合は「反復測定による一元配置分散分析」を用いることになる．そしてこれは「繰り返しのない二元配置分散分析」と同じである[1]
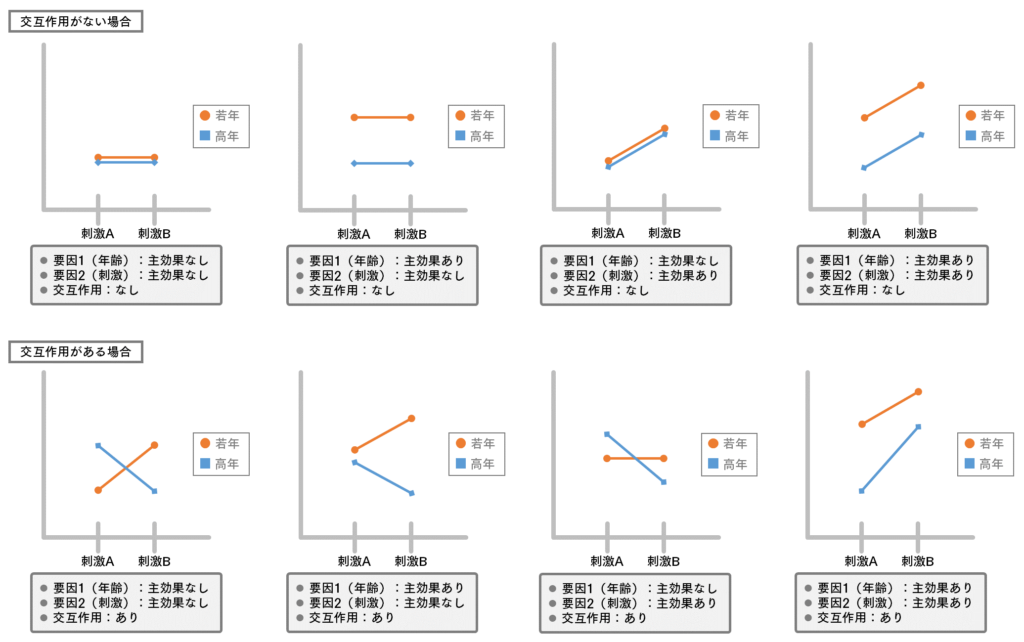
繰り返しのある二元配置分散分析に関し，図3の二元配置を基に，折れ線グラフで表した際の各主効果と交互作用の例を図4に示す．交互作用がない場合，各傾きが平行になる．これに対し，交互作用がある場合は，非平行になる．

反復測定と繰り返し測定
反復測定は，例えばある刺激という因子に対し，提示前・提示中・提示後に渡って反復した測定のことを呼ぶ．これは対応がある計測を表す（図5）
繰り返し測定は，ある実験やその同条件の測定を繰り返し行う測定のことを呼ぶ．これは対応がなく，別々の被験者からの計測を表す（図6）

独立変数と従属変数
独立変数は，要因または水準を表す．従属変数は，計測値を表す
多重比較との違い
分散分析は「全体の中で差異をもつものはあるか」を求められるが，その中の「群Aと群Bに違いがある」といった各群間での違いは求められない．そのため，3群以上の比較においては，分散分析などを行った後に，後述する多重比較を行う

名義尺度における比較

　前章までで説明した各検定では，順序尺度，間隔尺度，比例尺度に対して用いることができる検定である．本章では，名義尺度に対して使用可能な検定を上げる．

カイ二乗検定

使用例
「問．ふだん朝ご飯に何を食べるか？」「回答の選択肢．米，パン，シリアル，食べない」等の名義尺度のアンケート結果に対する比較
使用条件
母集団の分布：非正規分布でも可能
期待値：各期待値を算出する際に，各期待値がすべて5より大きいこと（近似計算であるため，データ数が少ないと使用できない）

Fisher（フィッシャー）の直接確率検定

使用例
「問．ふだん朝ご飯に何を食べるか？」「回答の選択肢．米，パン，シリアル，食べない」等の名義尺度のアンケート結果に対する比較
使用条件
母集団の分布：非正規分布でも可能
期待値：各期待値を算出する際に，期待値が5以下のものがあっても使用可能
その他：1元の表に対しては，Fisherの直接確率検定は使用できない（分割表のセルの周辺和を固定し、各セルの値を変化させて確率を計算する手法のため）

多重比較

　3群以上の比較など複数回比較を行う場合は，複数回の比較を行っても設定した有意水準で判定するよう補正をかける必要がある．これを加味した検定を多重比較といい，下記の様な検定法がある（図7）．

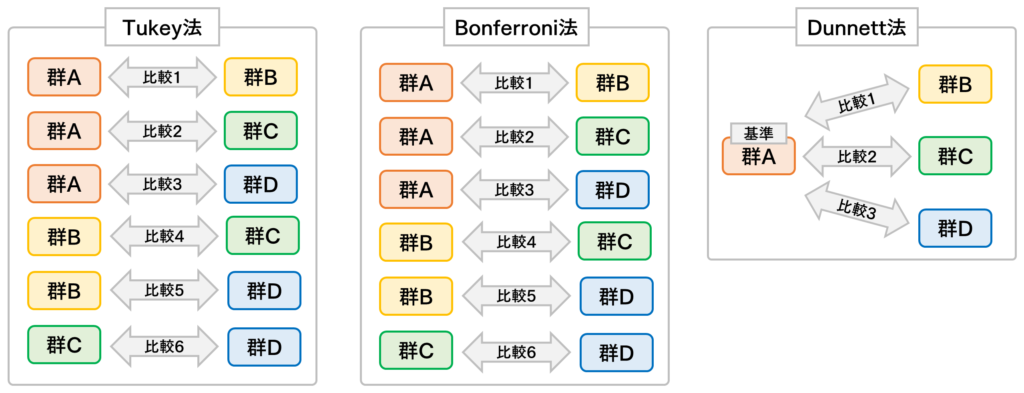
Tukey（テューキー）法

概要
全群の組み合わせで比較
使用条件
母集団の分布：正規分布
母分散：各群の母分散が等しい

Bonferroni（ボンフェローニ）法

概要
全群の組み合わせで比較
Bonferroni法では，有意水準を比較回数で割ることで，複数回の検定を行っても有意水準を保つ．例えば4群で比較する場合，比較回数は6回となる．有意水準5%ならばそれを6で割り，約0.83%を各比較での有意水準とする．これにより，6回比較を行っても全体の有意水準は5%に保つ
使用条件
母集団の分布：非正規分布でも可能
母分散：各群の母分散が等しくなくとも可能

Holm（ホルム）法

概要
前述したBonferroni法は，比較回数で有意水準を割る．そのため，例えば5群間での比較においては比較回数は10回となり，各比較の有意水準は0.5%となる．このことからBonferroni法は，5群以上の比較においては厳しい検定になる（＝有意差が出づらい）と言われている
これに対し，p値に傾斜つけて緩和した検定法がHolm法らしい（第2種の過誤の観点もあるが，少なくとも「有意差が出づらい」という理由で検定法を選ぶことに筆者は懐疑的である．そのため，筆者はHolm法を用いたことはない）

Dunnett（ダネット）法

概要
基準となる群に対する，複数の他群との比較（＝全群の組み合わせによる総当たりではない）
使用条件
母集団の分布：正規分布
母分散：各群の母分散が等しい

参考文献

池田郁男: 統計検定を理解せずに使っている人のためにIII, 化学と生物, Vol.51, No.7, pp.483-495(2013).

目次